快速开始

AI Studio快速体验

本文通过一个简单的 demo 及其扩展问题，介绍如何使用 PaddleScience 训练模型，解决一类方程学习与预测问题，并可视化预测结果。

1. 问题简介

假设我们希望用神经网络模型去拟合 \(x \in [-\pi, \pi]\) 区间内，\(u=\sin(x)\) 这一函数。在拟合函数已知和未知两种情形下，如何去尽可能地准确拟合 \(u=\sin(x)\)。

第一种场景下，假设已知目标函数 \(u\) 的解析解就是 \(u=\sin(x)\)，我们采用监督训练的思路，直接用该公式生成标签因变量 \(u\)，与自变量 \(x\) 共同作为监督数据对模型进行训练。

第二种场景下，假设不知道目标函数 \(u\) 的解析解，但我们知道其满足某种微分关系，我们这里以其中一个满足条件的微分方程 \(\dfrac{\partial u} {\partial x}=\cos(x)\) 为例，介绍如何生成数据进行训练。

2. 场景一

目标拟合函数：

\[ u=\sin(x), x \in [-\pi, \pi]. \]

我们生成 \(N\) 组数据对 \((x_i, u_i), i=1,...,N\) 作为监督数据进行训练即可。

在撰写代码之前，我们首先导入必要的包。

import numpy as np
import paddle

import ppsci
from ppsci.utils import logger

然后创建日志和模型保存目录供训练过程记录和保存使用，这一步是绝大部分案例在正式开始前都需要进行的操作。

# set random seed for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case1"

# initialize logger
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

接下来正式开始撰写代码。

首先定义问题区间，我们使用 ppsci.geometry.Interval 定义一个线段几何形状，方便后续在该线段上对 \(x\) 进行采样。

# set input 1D-geometry([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)
geom = {"domain": x_domain}

然后定义一个简单的 3 层 MLP 模型。

# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

上述代码表示模型接受自变量 \(x\) 作为输入，输出预测结果 \(\hat{u}\)

然后我们定义已知的 \(u=\sin(x)\) 计算函数，作为 ppsci.constraint.InteriorConstraint 的参数，用于生成标签数据，InteriorConstraint 表示以给定的几何形状或数据集中的数据作为输入，联合给定的标签数据，指导模型进行优化。

# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])

# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"u": lambda out: out["u"]},
    label_dict={"u": sin_compute_func},
    geom=geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,
    },
    loss=ppsci.loss.MSELoss(),
)
# wrap constraint(s) into one dict
constraint = {interior_constraint.name: interior_constraint}

此处的 interior_constraint 表示一个训练目标，即我们希望在 \([-\pi, \pi]\) 这段区间内，优化模型让模型的预测结果 \(\hat{u}\) 尽可能地接近它的标签值 \(u\)。

接下来就可以开始定义模型训练相关的内容，比如训练轮数、优化器

# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(1e-3)(model)

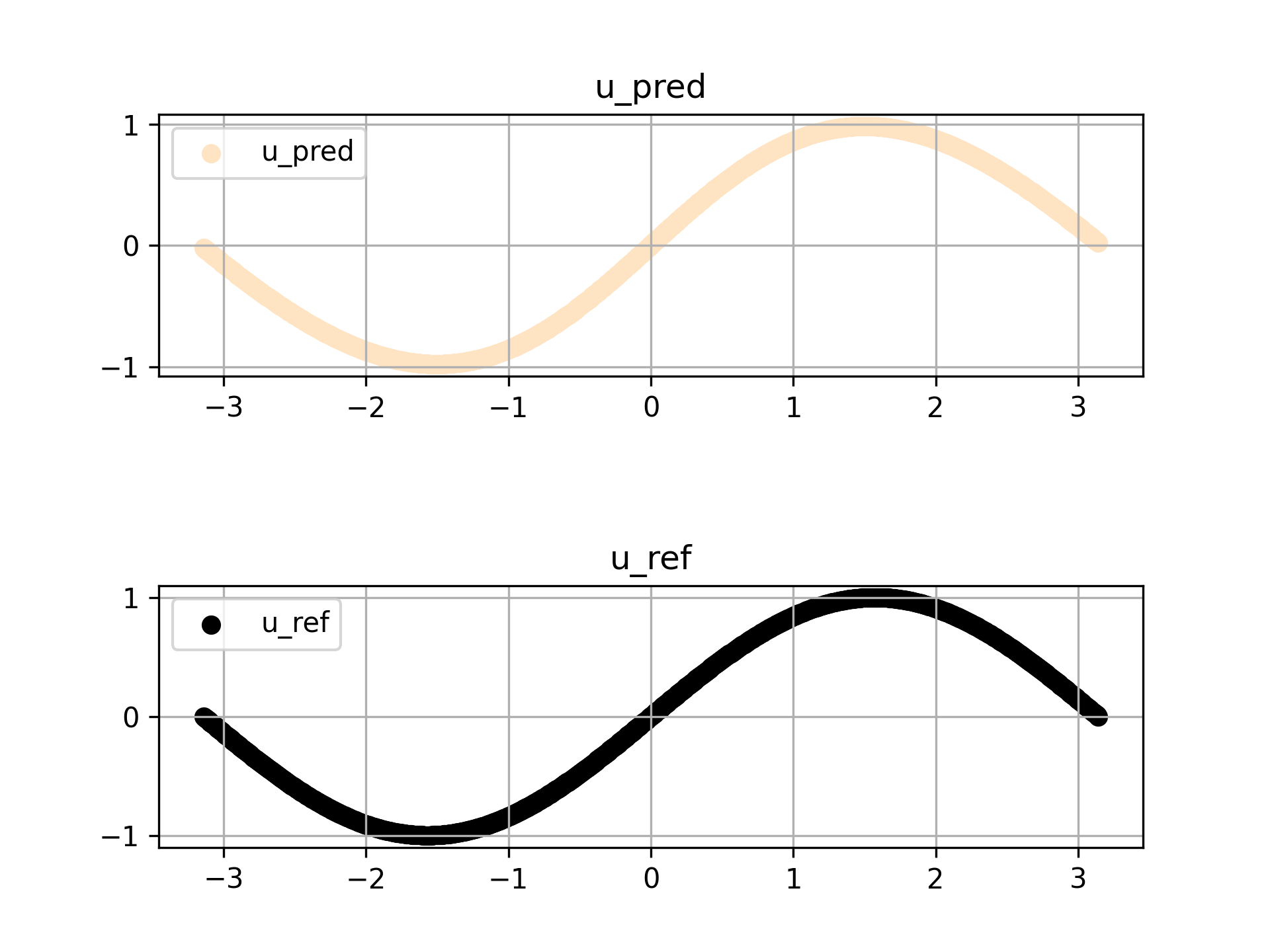
当训练完成，我们希望在 \([-\pi, \pi]\) 上取 1000 个点进行预测并将结果可视化，以此查看训练完毕的模型是否具备一定的预测能力。

# set visualizer
visualize_input_dict = {"x": paddle.linspace(l_limit, r_limit, 1000).reshape([1000, 1])}
visualize_input_dict["u_ref"] = paddle.sin(visualize_input_dict["x"])
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visualize_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

最后将上述定义的对象传递给训练调度类 Solver，即可开始模型训练

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    geom=geom,
    visualizer=visualizer,
)
# train model
solver.train()

训练完毕后再用刚才取的 1000 个点进行可视化

# visualize prediction after finished training
solver.visualize()

训练记录下所示

...
...
ppsci INFO: [Train][Epoch 10/10][Iter: 60/100] lr: 0.00100000, loss: 0.00084, EQ: 0.00084, batch_cost: 0.00193s, reader_cost: 0.00017s, ips: 16607.08697 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 70/100] lr: 0.00100000, loss: 0.00082, EQ: 0.00082, batch_cost: 0.00193s, reader_cost: 0.00016s, ips: 16603.29541 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 80/100] lr: 0.00100000, loss: 0.00078, EQ: 0.00078, batch_cost: 0.00193s, reader_cost: 0.00016s, ips: 16612.34228 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 90/100] lr: 0.00100000, loss: 0.00076, EQ: 0.00076, batch_cost: 0.00193s, reader_cost: 0.00015s, ips: 16616.61847 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 100/100] lr: 0.00100000, loss: 0.00075, EQ: 0.00075, batch_cost: 0.00191s, reader_cost: 0.00015s, ips: 16715.53436 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Avg] loss: 0.00075, EQ: 0.00075
ppsci INFO: Finish saving checkpoint to ./output_quick_start_case1/checkpoints/latest
ppsci INFO: 1D result is saved to ./output_quick_start_case1/visual/epoch_0/u=sin(x).png
ppsci INFO: [Visualize][Epoch 0] Finished visualization.

预测结果如下所示

场景一的完整代码如下所示

import numpy as np
import paddle

import ppsci
from ppsci.autodiff import jacobian
from ppsci.utils import logger

# set random seed for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case1"

# initialize logger
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

# set input 1D-geometry([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)
geom = {"domain": x_domain}

# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])

# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"u": lambda out: out["u"]},
    label_dict={"u": sin_compute_func},
    geom=geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,
    },
    loss=ppsci.loss.MSELoss(),
)
# wrap constraint(s) into one dict
constraint = {interior_constraint.name: interior_constraint}

# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(1e-3)(model)

# set visualizer
visualize_input_dict = {"x": paddle.linspace(l_limit, r_limit, 1000).reshape([1000, 1])}
visualize_input_dict["u_ref"] = paddle.sin(visualize_input_dict["x"]) + 2
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visualize_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    geom=geom,
    visualizer=visualizer,
)
# train model
solver.train()

# visualize prediction after finished training
solver.visualize()

3. 场景二

可以看到场景一的监督训练方式能较好地解决函数拟合问题，但一般情况下我们是无法得知拟合函数本身的解析式的，因此也无法直接构造因变量的监督数据。

虽然无法求出解析式直接构造监督数据，但往往可以利用相关数学知识，推导出目标拟合函数符合的某种数学关系，以训练模型以满足这种数学关系的方式，达到以“间接监督”的方式优化模型的目的。

假设我们不再使用 \(u=\sin(x)\) 这一先验公式，因而无法生成标签数据 \(u\)。因此我们使用如下方程组，其含有一个偏微分方程和边界条件

\[ \begin{cases} \begin{aligned} \dfrac{\partial u} {\partial x} &= \cos(x) \\ u(-\pi) &= 2 \end{aligned} \end{cases} \]

构造数据对 \((x_i, \cos(x_i)), i=1,...,N\)。 这意味着我们仍然能保持模型的输入、输出不变，但优化目标变成了：让 \(\dfrac{\partial \hat{u}} {\partial x}\) 尽可能地接近 \(\cos(x)\)，且 \(\hat{u}(-\pi)\) 也要尽可能地接近 \(2\)。

基于以上理论，我们对场景一的代码进行少量的改写即可得到本场景二的代码。

首先由于我们需要使用一阶微分这一操作，因此在代码开头处需导入一阶微分 API

import numpy as np
import paddle

import ppsci
from ppsci.autodiff import jacobian
from ppsci.utils import logger

然后将原来的标签生成函数改为微分关系标签生成函数

# standard solution of cos(x)
def cos_compute_func(data: dict):
    return np.cos(data["x"])

接着将 interior_constraint 这一约束条件从约束“模型输出”，改为约束“模型输出对输入的一阶微分”

interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"du_dx": lambda out: jacobian(out["u"], out["x"])},
    label_dict={"du_dx": cos_compute_func},
    geom=geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,
    },
    loss=ppsci.loss.MSELoss(),
)

考虑到一般情况下偏微分方程的解会存在待定系数，需通过定解条件（初（边）值条件）来确定，因此需要在 interior_constraint 构建代码的后面，额外添加一个边界条件约束，如下所示

bc_constraint = ppsci.constraint.BoundaryConstraint(
    {"u": lambda d: d["u"]},
    {"u": lambda d: sin_compute_func(d) + 2}, # (1)
    geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 1,
    },
    loss=ppsci.loss.MSELoss(),
    criteria=lambda x: np.isclose(x, l_limit), # only choose x close to l_limit, i.e. -pi
)

1. 对应边界条件 \(u(x_0)=sin(x_0)+2\)

然后将该边界约束添加到 constraint 中

# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
    bc_constraint.name: bc_constraint,
}

同样地，修改 Visualizer 绘制的标准解为 \(sin(x)+2\)

# set visualizer
visualize_input_dict = {"x": paddle.linspace(l_limit, r_limit, 1000).reshape([1000, 1])}
visualize_input_dict["u_ref"] = paddle.sin(visualize_input_dict["x"]) + 2
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visualize_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)+2",
    ),
}

修改完毕后执行训练

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    geom=geom,
    visualizer=visualizer,
)
# train model
solver.train()

训练日志如下所示

...
...
ppsci INFO: [Train][Epoch 10/10][Iter: 70/100] lr: 0.00100000, loss: 0.00035, EQ: 0.00035, batch_cost: 0.01183s, reader_cost: 0.00017s, ips: 2705.18917 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 80/100] lr: 0.00100000, loss: 0.00035, EQ: 0.00035, batch_cost: 0.01133s, reader_cost: 0.00017s, ips: 2823.74760 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 90/100] lr: 0.00100000, loss: 0.00036, EQ: 0.00036, batch_cost: 0.01141s, reader_cost: 0.00017s, ips: 2803.77351 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter: 100/100] lr: 0.00100000, loss: 0.00036, EQ: 0.00036, batch_cost: 0.01106s, reader_cost: 0.00016s, ips: 2892.93859 samples/s, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Avg] loss: 0.00036, EQ: 0.00036
ppsci INFO: Finish saving checkpoint to ./output_quick_start_case2/checkpoints/latest
ppsci INFO: 1D result is saved to ./output_quick_start_case2/visual/epoch_0/u=sin(x)+2.png
ppsci INFO: [Visualize][Epoch 0] Finished visualization.

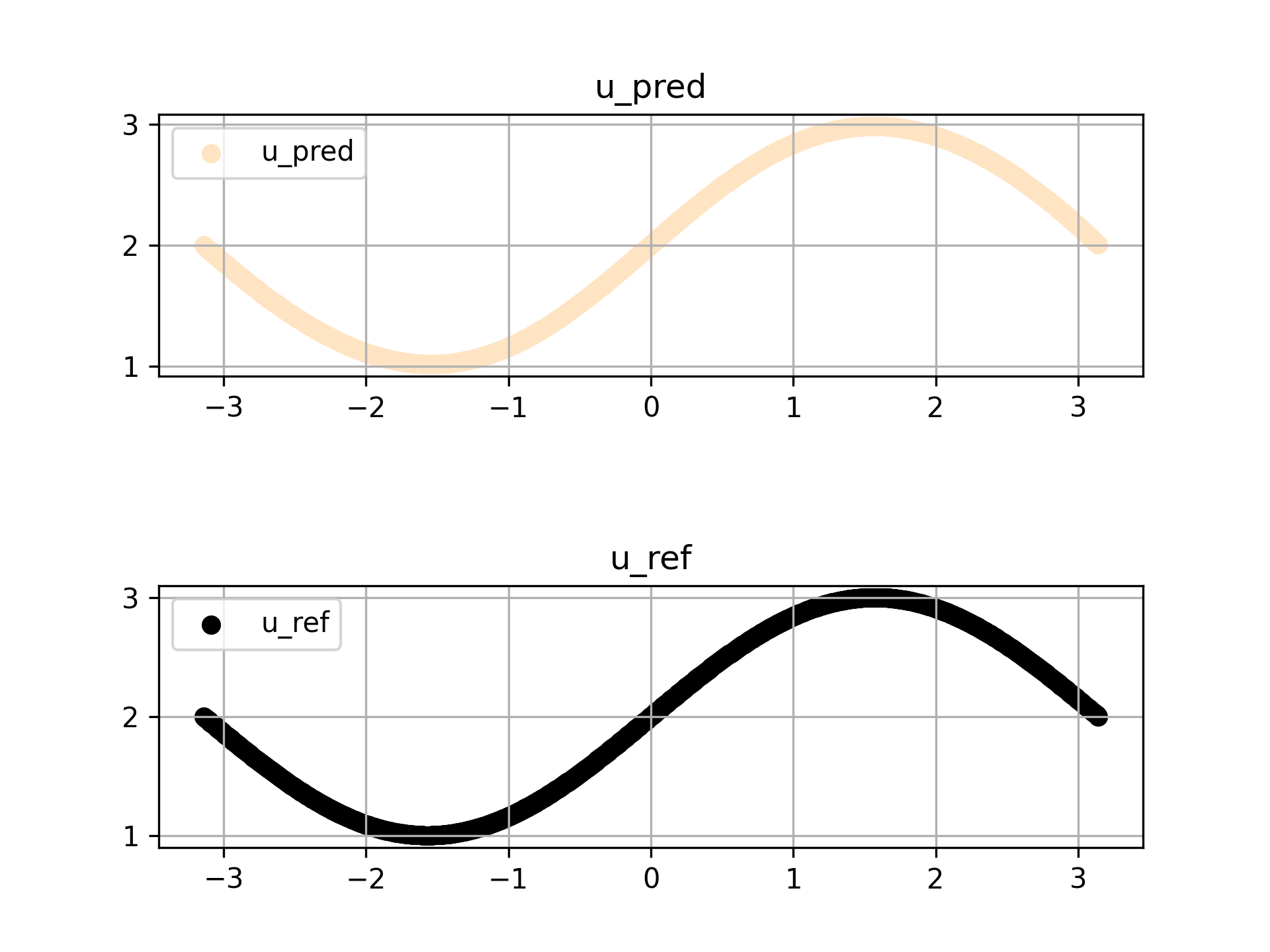
预测结果如下所示

可以发现利用微分关系训练的模型仍然具备良好的预测能力，并且结合定解条件，能学习出同时符合微分方程和定解条件的正确解模型。

场景二的完整代码如下所示

import numpy as np
import paddle

import ppsci
from ppsci.autodiff import jacobian
from ppsci.utils import logger

# set random seed for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case2"

# initialize logger
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

# set input 1D-geometry([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)
geom = {"domain": x_domain}

# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])

# standard solution of cos(x)
def cos_compute_func(data: dict):
    return np.cos(data["x"])

# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"du_dx": lambda out: jacobian(out["u"], out["x"])},
    label_dict={"du_dx": cos_compute_func},
    geom=geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,
    },
    loss=ppsci.loss.MSELoss(),
)
bc_constraint = ppsci.constraint.BoundaryConstraint(
    {"u": lambda d: d["u"]},
    {"u": lambda d: sin_compute_func(d) + 2},
    geom["domain"],
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 1,
    },
    loss=ppsci.loss.MSELoss(),
    criteria=lambda x: np.isclose(x, l_limit),
)
# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
    bc_constraint.name: bc_constraint,
}

# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(1e-3)(model)

# set visualizer
visualize_input_dict = {"x": paddle.linspace(l_limit, r_limit, 1000).reshape([1000, 1])}
visualize_input_dict["u_ref"] = paddle.sin(visualize_input_dict["x"]) + 2
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visualize_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    geom=geom,
    visualizer=visualizer,
)
# train model
solver.train()

# visualize prediction after finished training
solver.visualize()

---

最后更新: November 6, 2023
创建日期: November 6, 2023