PhyCRNet

AI Studio快速体验

模型训练命令模型评估命令

# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyCRNet/burgers_1501x2x128x128.mat -P ./data/

# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyCRNet/burgers_1501x2x128x128.mat --output ./data/burgers_1501x2x128x128.mat

python main.py DATA_PATH=./data/burgers_1501x2x128x128.mat

# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyCRNet/burgers_1501x2x128x128.mat -P ./data/
# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyCRNet/burgers_1501x2x128x128.mat --output ./data/burgers_1501x2x128x128.mat

python main.py mode=eval DATA_PATH=./data/burgers_1501x2x128x128.mat EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/phycrnet/phycrnet_burgers.pdparams

预训练模型	指标
phycrnet_burgers_pretrained.pdparams	a-RMSE: 3.20e-3

1. 背景简介

复杂时空系统通常可以通过偏微分方程（PDE）来建模，它们在许多领域都十分常见，如应用数学、物理学、生物学、化学和工程学。求解PDE系统一直是科学计算领域的一个关键组成部分。 本文的具体目标是为了提出一种新颖的、考虑物理信息的卷积-递归学习架构（PhyCRNet）及其轻量级变体（PhyCRNet-s），用于解决没有任何标签数据的多维时间空间PDEs。本项目主要目标是使用PaddleScience复现论文所提供的代码，并与代码的精度对齐。

该网络有以下优势：

1、 使用ConvLSTM(enconder-decoder Convolutional Long Short-Term Memory network) 可以充分提取低维空间上的特征以及学习其时间上的变化。

2、使用一个全局的残差迭代从而可以严格地执行时间上的迭代过程。

3、使用基于高阶有限差分格式的滤波从而能够精确求解重要的偏微分方程导数值。

4、使用强制边界条件是的所求解的数值解可以满足原方程所要求的初值以及边界条件。

2. 问题定义

在本模型中，我们考虑的是含有时间和空间的PDE模型，此类模型在推理过程中会存在时间上的误差累积的问题，因此，本文通过设计循环卷积神经网络试图减轻每一步时间迭代的误差累积。而我们所求解的问题为以高斯分布随机得到的值为初值的二维Burgers' Equation：

\[u_t+u\cdot \nabla u -\nu u =0\]

二维Burgers' Equation 刻画了复杂的非线性的反应扩散相互作用的问题，因此，经常被用来当作benchmark来比较各种科学计算算法。

3. 问题求解

3.1 模型构建

在这一部分中，我们介绍 PhyCRNet 的架构，包括编码器-解码器模块、残差连接、自回归（AR）过程和基于过滤的微分。网络架构如图所示。编码器(黄色Encoder，包含3个卷积层)，用于从输入状态变量 \(u(t=i)，i = 0,1,2,..,T-1\) 学习低维潜在特征，其中 \(T\) 表示总时间步。我们应用 ReLU 作为卷积层的激活函数。然后，我们将ConvLSTM层的输出(Encoder得到的低分辨率)，潜在特征的时间传播器(绿色部分)，其中，输出的LSTM的记忆单元 \(C_i\) 和LSTM的隐藏变量单元 \(h_i\) 会作为下一个时间步的输入。这样做的好处是对低维变量的基本动态进行建模,能够准确地捕获时间依赖性，同时有助于减轻记忆负担。 使用 LSTM 的另一个优势来自输出状态的双曲正切函数，它可以保持平滑的梯度曲线，并将值控制在 -1 和 1 之间。在建立低分辨率LSTM卷积循环方案后，我们基于上采样操作Decoder(蓝色部分)直接将低分辨率潜在空间重建为高分辨率量。特别注明，应用了子像素卷积层（即像素shuffle），因为与反卷积相比，它具有更好的效率和重建精度，且伪像更少。 最后，我们添加另一个卷积层，用于将有界潜变量空间输出，缩放回原始的物理空间。该Decoder后面没有激活函数。 此外，值得一提的是，鉴于输入变量数量有限及其对超分辨率的缺陷，我们在 PhyCRNet 中没有考虑 batch normalization。 作为替代，我们使用 batch normalization 来训练网络，以实现训练加速和更好的收敛性。受到动力学中，Forward Eular Scheme 的启发，我们在输入状态变量 \(u_i\) 和输出变量 \(u_{i+1}\) 之间附加全局残差连接。具体网络结构如下图所示：

接下来，剩下的挑战是，如何进行物理嵌入，来融合N-S方程带来的精度提升。我们应用无梯度卷积滤波器，来表示离散数值微分，以近似感兴趣的导数项。 例如，我们在本文中考虑的基于 Finite Difference 有限差分的滤波器是2阶和4阶中心差分格式，来计算时间和空间导数。

时间差分:

\[K_t = [-1,0,1] \times \frac{1}{2 \delta t},\]

空间差分:

\[K_s = \begin{bmatrix} 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 16 & 0 & 0 \\ -1 & 16 & -60 & 16 & -1 \\ 0 & 0 & 16 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 \\ \end{bmatrix} \times \frac{1}{12 (\delta x)^2},\]

其中 \(\delta t\) 和 \(\delta x\) 表示时间步长和空间步长。

此外需要注意无法直接计算边界上的导数，丢失边界差异信息的风险可以通过接下来引入的在传统有限差分中经常使用的鬼点填充机制来减轻，其主要核心是在矩阵外围填充一层或多层鬼点（层数取决于差分格式，即，过滤器的大小），以下图为例，在迪利克雷边界条件（Dirichlet BCs）下，我们只需要把常值鬼点在原矩阵外围填充即可；在诺伊曼边界条件(Neumann BCs)下，我们需要根据其边界条件导数值确定鬼点的值。

    dt=cfg.DT, step=steps, effective_step=effective_step, **cfg.MODEL
)

# model settings
MODEL:
  input_channels: 2
  hidden_channels: [8, 32, 128, 128]
  input_kernel_size: [4, 4, 4, 3]
  input_stride: [2, 2, 2, 1]
  input_padding: [1, 1, 1, 1]
  num_layers: [3, 1]

3.2 数据载入

我们使用RK4或者谱方法生成的数据（初值为使用正态分布生成），需要从.mat文件中将其读入，：

uv = data["uv"]  # [t,c,h,w]
functions.uv = uv

# generate input data
(
    input_dict_train,
    label_dict_train,
    input_dict_val,
    label_dict_val,
) = functions.Dataset(
    paddle.to_tensor(initial_state),
    paddle.to_tensor(
        uv[
            0:1,
        ],
        dtype=paddle.get_default_dtype(),
    ),
).get()

3.3 约束构建

设置约束以及相关损失函数：

    {
        "dataset": {
            "name": "NamedArrayDataset",
            "input": input_dict_train,
            "label": label_dict_train,
        },
        "batch_size": 1,
        "num_workers": 0,
    },
    ppsci.loss.FunctionalLoss(functions.train_loss_func),
    {
        "loss": lambda out: out["loss"],
    },
    name="sup_train",
)
constraint_pde = {sup_constraint_pde.name: sup_constraint_pde}

3.4 评估器构建

设置评估数据集和相关损失函数：

    {
        "dataset": {
            "name": "NamedArrayDataset",
            "input": input_dict_val,
            "label": label_dict_val,
        },
        "batch_size": 1,
        "num_workers": 0,
    },
    ppsci.loss.FunctionalLoss(functions.val_loss_func),
    {
        "loss": lambda out: out["loss"],
    },
    metric={"metric": ppsci.metric.FunctionalMetric(functions.metric_expr)},
    name="sup_valid",
)
validator_pde = {sup_validator_pde.name: sup_validator_pde}

3.6 优化器构建

训练过程会调用优化器来更新模型参数，此处选择 Adam 优化器并设定 learning_rate

optimizer = ppsci.optimizer.Adam(scheduler)(model)
solver = ppsci.solver.Solver(
    model,
    constraint_pde,

3.7 模型训练与评估

为了评估所有基于神经网络的求解器产生的解决方案精度，我们分两个阶段评估了全场误差传播：训练和外推。在时刻 τ 的全场误差 \(\epsilon_\tau\) 的定义为给定 b 的累积均方根误差 (a-RMSE)。

\[ \epsilon_\tau=\sqrt{\frac{1}{N_\tau} \sum_{k=1}^{N_\tau} \frac{\left\|\mathbf{u}^*\left(\mathbf{x}, t_k\right)-\mathbf{u}^\theta\left(\mathbf{x}, t_k\right)\right\|_2^2}{m n}} \]

这一步需要通过设置外界函数来进行，因此在训练过程中，我们使用function.transform_out来进行训练

    return functions.transform_out(_in, _out, model)

model.register_input_transform(functions.transform_in)
model.register_output_transform(_transform_out)

而在评估过程中，我们使用function.tranform_output_val来进行评估，并生成累计均方根误差。

(h0, c0) = (paddle.randn((1, 128, 16, 16)), paddle.randn((1, 128, 16, 16)))

完成上述设置之后，只需要将上述实例化的对象按顺序传递给 ppsci.solver.Solver。

    cfg.output_dir,
    optimizer,
    scheduler,
    cfg.TRAIN.epochs,
    cfg.TRAIN.iters_per_epoch,
    validator=validator_pde,
    eval_with_no_grad=cfg.TRAIN.eval_with_no_grad,
    pretrained_model_path=cfg.TRAIN.pretrained_model_path,
)

# train model
solver.train()
# evaluate after finished training

最后启动训练、评估即可：

def evaluate(cfg: DictConfig):
    # set random seed for reproducibility
    ppsci.utils.misc.set_random_seed(cfg.seed)
    # initialize logger
    logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info")

    # set initial states for convlstm

4. 完整代码

"""
PhyCRNet for solving spatiotemporal PDEs
Reference: https://github.com/isds-neu/PhyCRNet/
"""
from os import path as osp

import functions
import hydra
import paddle
import scipy.io as scio
from omegaconf import DictConfig

import ppsci
from ppsci.utils import logger


def train(cfg: DictConfig):
    # set random seed for reproducibility
    ppsci.utils.misc.set_random_seed(cfg.seed)
    # initialize logger
    logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info")

    # set initial states for convlstm
    NUM_CONVLSTM = cfg.num_convlstm
    (h0, c0) = (paddle.randn((1, 128, 16, 16)), paddle.randn((1, 128, 16, 16)))
    initial_state = []
    for _ in range(NUM_CONVLSTM):
        initial_state.append((h0, c0))

    # grid parameters
    time_steps = cfg.TIME_STEPS
    dx = cfg.DX[0] / cfg.DX[1]

    steps = cfg.TIME_BATCH_SIZE + 1
    effective_step = list(range(0, steps))
    num_time_batch = int(time_steps / cfg.TIME_BATCH_SIZE)

    functions.dt = cfg.DT
    functions.dx = dx
    functions.time_steps = cfg.TIME_STEPS
    functions.num_time_batch = num_time_batch
    model = ppsci.arch.PhyCRNet(
        dt=cfg.DT, step=steps, effective_step=effective_step, **cfg.MODEL
    )

    def _transform_out(_in, _out):
        return functions.transform_out(_in, _out, model)

    model.register_input_transform(functions.transform_in)
    model.register_output_transform(_transform_out)

    # use Burgers_2d_solver_HighOrder.py to generate data
    data = scio.loadmat(cfg.DATA_PATH)
    uv = data["uv"]  # [t,c,h,w]
    functions.uv = uv

    # generate input data
    (
        input_dict_train,
        label_dict_train,
        input_dict_val,
        label_dict_val,
    ) = functions.Dataset(
        paddle.to_tensor(initial_state),
        paddle.to_tensor(
            uv[
                0:1,
            ],
            dtype=paddle.get_default_dtype(),
        ),
    ).get()

    sup_constraint_pde = ppsci.constraint.SupervisedConstraint(
        {
            "dataset": {
                "name": "NamedArrayDataset",
                "input": input_dict_train,
                "label": label_dict_train,
            },
            "batch_size": 1,
            "num_workers": 0,
        },
        ppsci.loss.FunctionalLoss(functions.train_loss_func),
        {
            "loss": lambda out: out["loss"],
        },
        name="sup_train",
    )
    constraint_pde = {sup_constraint_pde.name: sup_constraint_pde}

    sup_validator_pde = ppsci.validate.SupervisedValidator(
        {
            "dataset": {
                "name": "NamedArrayDataset",
                "input": input_dict_val,
                "label": label_dict_val,
            },
            "batch_size": 1,
            "num_workers": 0,
        },
        ppsci.loss.FunctionalLoss(functions.val_loss_func),
        {
            "loss": lambda out: out["loss"],
        },
        metric={"metric": ppsci.metric.FunctionalMetric(functions.metric_expr)},
        name="sup_valid",
    )
    validator_pde = {sup_validator_pde.name: sup_validator_pde}

    # initialize solver
    scheduler = ppsci.optimizer.lr_scheduler.Step(**cfg.TRAIN.lr_scheduler)()

    optimizer = ppsci.optimizer.Adam(scheduler)(model)
    solver = ppsci.solver.Solver(
        model,
        constraint_pde,
        cfg.output_dir,
        optimizer,
        scheduler,
        cfg.TRAIN.epochs,
        cfg.TRAIN.iters_per_epoch,
        validator=validator_pde,
        eval_with_no_grad=cfg.TRAIN.eval_with_no_grad,
        pretrained_model_path=cfg.TRAIN.pretrained_model_path,
    )

    # train model
    solver.train()
    # evaluate after finished training
    model.register_output_transform(functions.tranform_output_val)
    solver.eval()


def evaluate(cfg: DictConfig):
    # set random seed for reproducibility
    ppsci.utils.misc.set_random_seed(cfg.seed)
    # initialize logger
    logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info")

    # set initial states for convlstm
    NUM_CONVLSTM = cfg.num_convlstm
    (h0, c0) = (paddle.randn((1, 128, 16, 16)), paddle.randn((1, 128, 16, 16)))
    initial_state = []
    for _ in range(NUM_CONVLSTM):
        initial_state.append((h0, c0))

    # grid parameters
    time_steps = cfg.TIME_STEPS
    dx = cfg.DX[0] / cfg.DX[1]

    steps = cfg.EVAL.TIME_BATCH_SIZE + 1
    effective_step = list(range(0, steps))
    num_time_batch = int(time_steps / cfg.EVAL.TIME_BATCH_SIZE)

    functions.dt = cfg.DT
    functions.dx = dx
    functions.num_time_batch = num_time_batch
    model = ppsci.arch.PhyCRNet(
        dt=cfg.DT, step=steps, effective_step=effective_step, **cfg.MODEL
    )

    def _transform_out(_in, _out):
        return functions.transform_out(_in, _out, model)

    model.register_input_transform(functions.transform_in)
    model.register_output_transform(_transform_out)

    # use the generated data
    data = scio.loadmat(cfg.DATA_PATH)
    uv = data["uv"]  # [t,c,h,w]
    functions.uv = uv
    _, _, input_dict_val, _ = functions.Dataset(
        paddle.to_tensor(initial_state),
        paddle.to_tensor(uv[0:1, ...], dtype=paddle.get_default_dtype()),
    ).get()
    ppsci.utils.load_pretrain(model, cfg.EVAL.pretrained_model_path)
    model.register_output_transform(None)
    functions.output_graph(model, input_dict_val, cfg.output_dir, cfg.case_name)


@hydra.main(
    version_base=None, config_path="./conf", config_name="burgers_equations.yaml"
)
def main(cfg: DictConfig):
    if cfg.mode == "train":
        train(cfg)
    elif cfg.mode == "eval":
        evaluate(cfg)
    else:
        raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'")


if __name__ == "__main__":
    main()

5. 结果展示

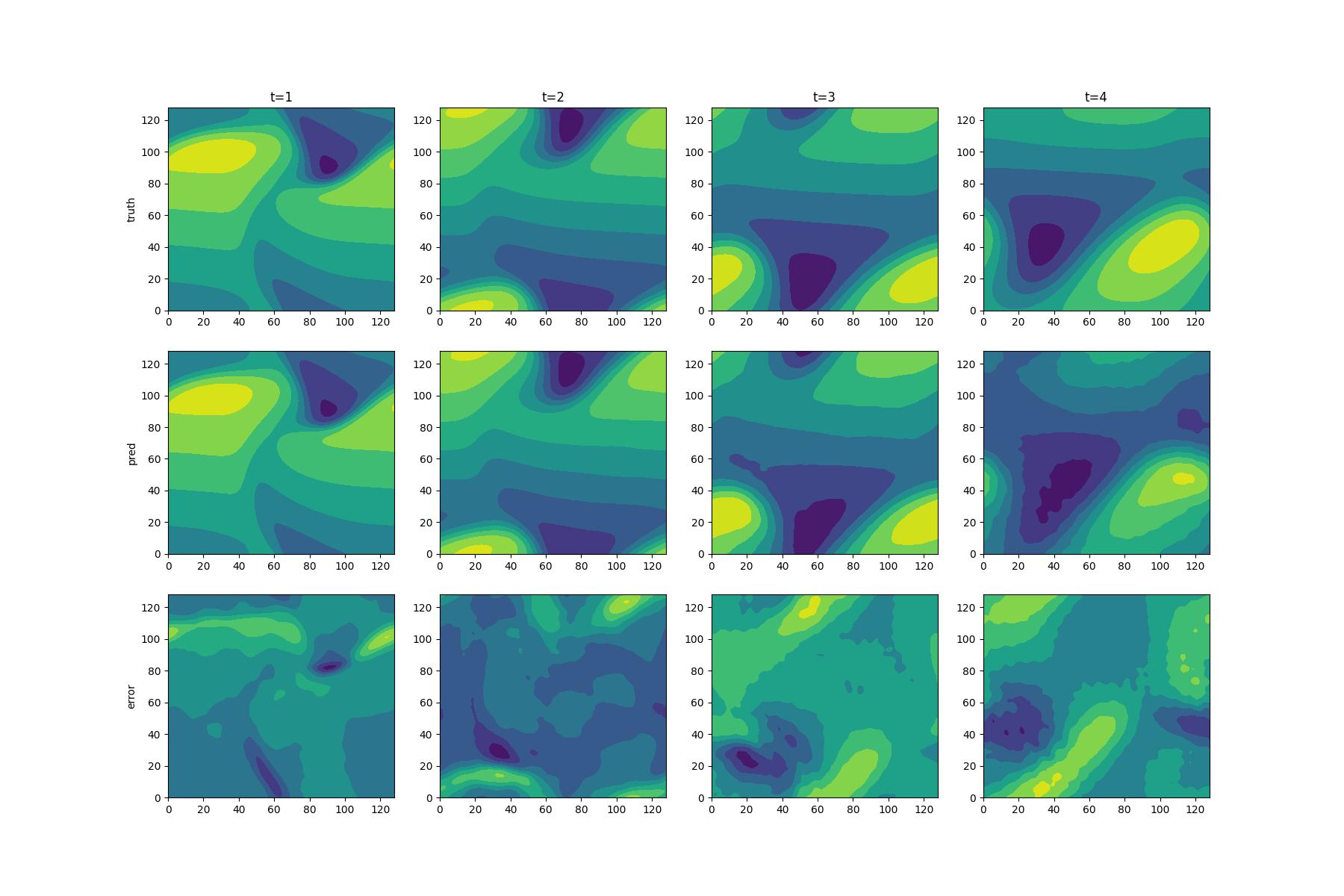
本文通过对Burgers' Equation进行训练，所得结果如下，根据精度和扩展能力的对比我们可以得出，我们的模型在训练集（t=1.0,2.0）以及拓展集（t=3.0,4.0）上均有良好的表现效果。pred为使用网络预测的速度的第一分量u在定义域上的contour图，truth为真实的速度第一分量u在定义域上的contour图，Error为预测值与真实值之间在整个定义域差值。

6. 结果说明

求解偏微分方程是在科学计算中的一个基本问题，而神经网络求解偏微分方程在求解逆问题以及数据同化问题等在传统方法上具有挑战性的问题上具有显著效果，但是，现有神经网络求解方法受限制于可扩展性，误差传导以及泛化能力等问题。因此，本论文通过提出一个新的神经网络PhyCRNet,通过将传统有限差分的思路嵌入物理信息神经网络中，针对性地解决原神经网络缺少对长时间数据的推理能力、误差累积以及缺少泛化能力的问题。与此同时，本文通过类似于有限差分的边界处理方式，将原本边界条件的软限制转为硬限制，大大提高了神经网络的准确性。新提出的网络可以有效解决上述提到的数据同化问题以及逆问题。

7. 参考资料

• PhyCRNet: Physics-informed Convolutional-Recurrent Network for Solving Spatiotemporal PDEs
• https://github.com/isds-neu/PhyCRNet